☰
matematika1
Suma reda s logaritmima
NIZOVI I REDOVI
Nužan uvjet konvergencije reda
Suma reda rastavljanjem na parcijalne razlomke
Izračunajte sume sljedećih redova:
- a)
-
 ,
,
- b)
-
![$ \displaystyle\sum_{n=1}^{\infty}
\left[\frac{n!-(n+2)!}{(n+3)!}\,(n+1)+\frac{n+1}{n+3}\right]$](img3013.gif) .
.
Rješenje.
- a)
- Opći član zadanog reda možemo zapisati u obliku
gdje je  aritmetički niz s općim članom
aritmetički niz s općim članom  . Rastavljanjem na parcijalne razlomke (vidi zadatak 6.10) slijedi
. Rastavljanjem na parcijalne razlomke (vidi zadatak 6.10) slijedi
pa je  -ta parcijalna suma jednaka
-ta parcijalna suma jednaka
Prema
![[*]](../icons.gif/crossref.gif) [M1, definicija 6.9], suma reda je
[M1, definicija 6.9], suma reda je
- b)
- Opći član zadanog reda jednak je
Rastavljanjem dobivenog izraza na parcijalne razlomke (vidi zadatak 6.10) slijedi
Sada  -tu parcijalnu sumu reda možemo zapisati u obliku
-tu parcijalnu sumu reda možemo zapisati u obliku
pa ukidanjem i primjenom
![[*]](../icons.gif/crossref.gif) [M1, definicija 6.9], slijedi da je suma reda jednaka
[M1, definicija 6.9], slijedi da je suma reda jednaka
Suma reda s logaritmima
NIZOVI I REDOVI
Nužan uvjet konvergencije reda
 ,
,
![$ \displaystyle\sum_{n=1}^{\infty}
\left[\frac{n!-(n+2)!}{(n+3)!}\,(n+1)+\frac{n+1}{n+3}\right]$](img3013.gif) .
.
 ,
,
![$ \displaystyle\sum_{n=1}^{\infty}
\left[\frac{n!-(n+2)!}{(n+3)!}\,(n+1)+\frac{n+1}{n+3}\right]$](img3013.gif) .
.




![$\displaystyle \quad +\left. \left(\frac{1}{3k-2}-\frac{1}{3k+1}\right)\right]$](img3019.gif)

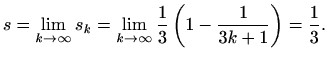

+\frac{n+1}{n+3}$](img3023.gif)



